 牌効率の概念 牌効率の概念
高い牌効率を身につける上において、最も大きな障壁を取り除かなければならない人は多い。それは、オカルトである。オカルト信者は、「索子の自摸が伸びているから索子を残す」とか「自摸に勢いがあるので辺張でも自摸れる」とか「あやっ牌が○○だからこれを残す」などということを基準に捨て牌選択を行う。このような無知蒙昧なことを信じていては、決して雀力は向上しない。
次に、「経験から学ぶ」「麻雀巧者の摸打を見て学ぶ」という姿勢の人が多いが、ある程度の雀力がついているならば、あまり効果はない。
何が必要かというと、パターン認識と計算による検証である。麻雀を打っているその場での計算はほぼ不可能である。捨て牌選択に迷った時に、その牌姿を覚えておいて、後でどちらの捨て牌選択が有効であったのかを計算し、検証することである。このような過程を経ずして雀力は向上しない。
「牌効率」と言う言葉は、「役を無視し、防御を無視して、ひたすら早く聴牌し和了すること」を指すこともあるが、ここでは、「防御は無視し、役は考慮した上で、最も早く高い手を和了すること」を「牌効率」と定義する。
現実的、実践的な論題として、「役を無視」ということはほぼあり得ないのである。
役を無視して早い和了だけを目指しても、麻雀は勝てない。和了には役が必要であるし、早く、高く和がるべきなのは当然である。
本来は、防御に関しても、無視、ということはあり得ないのであるが、待ち読みや抑えや絞りや回しに関しては、第3部に譲り、ここでは防御を外して、自分の手作りの効率性を論じることとする。
まず、最初は、基本的な局所的牌効率の比較例を示す。
たかだか5〜7牌程度の牌の効率すらも、正しく把握できていない人が多いからである。
・基本中の基本
    
最初は基本中の基本から。
5枚の牌を持っている。四五六萬で1面子、六七萬で両搭を構成している。五萬か八萬を自摸れば、面子ができる。
「五萬か八萬を自摸れ!」などと思っていても、そうは意図通りにはならず、六萬だったり七萬だったり四萬だったり三萬を自摸るものである。
     自摸: 自摸:
七萬を自摸ったら、四萬を切って、一盃口を目指すであろう。もちろん、門前であり、他の役が関係なければ、の話であるが。
     自摸: 自摸:
四萬を自摸ったら、門前で一盃口を確定させたいのなら七萬切り、平和があるなら平和を消す必要はなく、四萬の自摸切り。これも他の役が関係なければ、の話である。
ここで、平和があるのに、一盃口にこだわって平和を消すのは愚かな行為である。一盃口も平和も1飜であり、符の違いはあれど同じ1飜なら両面待ちの平和にするべきである。
     自摸: 自摸:
三萬を自摸ったら、面子構成に関係ないから自摸切り・・・・してしまう人もいるのである。大事なことに気づいていない。「五萬か八萬を自摸れ!」などと念じている人に限ってこのような重大なミスを犯す。
これは基本中の基本の形である。両面待ちが3面待ちに変わる形なのである。
六萬を切れば、五八萬待ちが、二五八萬になる。
「そんな簡単なことくらい判るよ」という声が聞こえてくるが、ここに対子や暗刻が混じっていると、その判断を誤って、待ちを少なくしている人は多いように感じる。
・単純に、嵌張から両面なのか?
    
と持っている。三五萬の嵌搭と、六七八萬の暗順である。「嵌張の四萬待ちだな」と認識するであろう。
この牌姿から、「嵌張四萬を自摸れ!」と念じても、そうはうまく入らないのが現実である。
ここで六萬を引いた時と、七萬を引いた時の違いについての面子・搭子認識について述べる。
六萬と七萬ではどちらがどれだけ有効であるか? 「どちらも嵌張待ちが両面待ちに変わるだけだから同じ」と思っている人は、牌効率の悪い人である。
(1)六萬自摸の場合
     
六萬を引いた時には、向聴数を減少させる有効牌が、四萬から四七萬に変わる。三萬はもしその後に四萬を引いた時に、三六九萬の3面待ちになる可能性を残すが、面子の確定性から考えると三萬は浮き牌になるのである。この萬子以外の他の面子・搭子・浮き牌と比較し、牌連続エネルギーを損なわないように打つべきであることは当然である。
(2)七萬自摸の場合
     
七萬を引いた時には、向聴数を減少させる有効牌が、四萬から六九萬に変わる、と考えてはいけない。
この形は、さきほどの六萬を引いて「四萬から四七萬に変わる」形とは全く違うのである。
この後、四萬を自摸れば、七萬を切って2面子完成なのである。この時には、三萬が必要になる。三萬は浮き牌ではない。つまり、向聴数を減少させる有効牌が、四萬から四六九萬に変わるのである。牌効率の悪い人はそれに気づかずに、三萬を切ってしま
う。そして振聴となるのである。ここで三萬を切って振聴にするのは裏目とか自摸が悪いとかいう問題ではない。牌効率が悪い、下手な打ち方の典型なのである。
七萬を引いた場合には、先ほどの六萬を引いた場合と比較して、三萬ははるかに重要な牌になるのである。
話を単純にすると、「六萬引いたら三萬打ってよし、七萬引いたら三萬は打つな」なのである。
・辺搭と浮き牌
  
ここから1枚切るとしたら、何を切るか?
単純だが、難しい論題、辺搭か浮き牌か、というものである。
浮き牌論者の主張はこうである。辺搭の愚形を残しても結局使えない。面子として成り立たない。少なくとも五筒のようなど真ん中の牌を持っていれば、三四五六七筒(5種19牌)のどれを
引いても搭子または対子になるし、最低でも辺搭よりましな嵌搭はできる。さらに一旦嵌搭ができてもその後に両搭に進化しうる。
一方、辺搭論者の主張はこうである。辺搭は愚形なれど搭子は搭子であり、これを崩してしまうことは、向聴数を増加させることとなる。麻雀は向聴数を減少させていくもの、それに逆行することは不利である。辺搭を崩した後で三萬を自摸って来たら目も当てられない。また、今は辺搭であるが、四萬を自摸って一萬を切って嵌搭へ、そして五萬を自摸って二萬を切って両搭へ、と進化しうる。
この牌効率を定量的に比較するために、以下の前提条件を設ける。
・ドラは論外とする。
・3回の自摸を想定し、それによって、今持っている牌を含めて面子ができるまでの回数と確率を求める。
・1回目の自摸で面子ができる場合(五筒を切って三萬を自摸る場合のみ)、その時点で終了とする。
・2回目の自摸で面子ができる場合も、その時点で終了とする。
・1回目の自摸は、手残りの2牌に関連する牌(最低嵌搭ができる牌)とする。
・最初に切った牌の関連牌は自摸切りするものとする。→要検討
・2回目の自摸も、手残りの2牌に関連する牌(最低嵌搭ができる牌)とする。
・3回目の自摸は、面子ができる牌だけに限定する。
計算の結果、以下の結果を得た。
| | 1回目の自摸で
面子確定する確率 | 2回目の自摸で
面子確定する確率 | 3回目の自摸で
面子確定する確率 | 合計 |
一萬切りの場合
(辺搭を嫌う場合) | 0.00% | 0.99% | 0.26% | 1.25% |
五筒切りの場合
(辺搭を残す場合) | 3.92% | 0.50% | 0.07% | 4.50% |
辺搭において、辺三萬を1回で自摸る確率は3.92%、これは、1回目に六筒を引いて2回目に七筒を引く確率、0.155%の実に25倍である。五筒を残した場合、2回の自摸で面子が確定するパターンは7通りあるが全部合わせても0.99%であり1%にも満たない。
よって、合計値で見て圧倒的に、辺搭を残す方が有利、となる。
・・・と言い切れるかどうかは、この数値から何を読みとるか、に依存する。
2回目の自摸で面子確定する確率を比較すると、辺搭を嫌う方が約2倍高い。また、3回目の自摸で面子確定する確率を比較すると、辺搭を嫌う方が約4倍弱高い、のである。
あくまで辺三萬を1回で自摸る確率を無視すれば、辺搭を嫌う方が牌効率がよい。
一般に短期レンジで見れば辺搭残しであり、長期レンジで見れば辺搭落としである。つまり、向聴数が少ない時(例えば0向聴=聴牌時)には辺搭を残すし、序盤などで向聴数が多い時には辺搭を嫌うのである。
では、何向聴までなら、辺搭を嫌うべきなのかの定量化については、今後の研究課題とする。
この論題を定量的に検証するには、向聴数の異なるものの定量比較の技法が必要である。この技法が確立すると、このケースの応用として、向聴数を増やす判断基準(例えば面子多々の時に対子を切って雀頭を一時的になくして向聴数を上げることの是非)などについての明確な解答が可能になる。
・二嵌と両搭と暗刻
             
自摸状態。伏せ牌部分の6枚では、2面子ができているものとする。
両搭の筒子に手をかけるのはひどすぎる。萬子の二嵌を崩すか、三索の暗刻を落とすのか、であろう。
(1)三萬切り
聴牌に必要な牌は、五六七萬・二三四五筒の7種24牌である。
(2)三筒切り
聴牌に必要な牌は、三四六七萬・四筒の5種18牌である。
(3)三索切り
聴牌に必要な牌は、四六萬・二五筒の4種16牌である。
従って、圧倒的に三萬切り(七萬でも同様)が牌効率がよい。
暗刻は面子であり、この時点でこれを1枚切って雀頭にしようと考えるのは最も愚かである。両搭は面子構成寄与率が二嵌よりも高いので、二嵌を崩すのが正解となる。
・暗刻くっつき
              ドラ: ドラ:
自摸状態。伏せ牌部分の6枚では、2面子ができているものとする。ドラの西は残して打つことを前提とする。
五筒、六筒、四索のどれを切っても、二向聴。どれを切るか?
(1)五筒切り
一向聴になる有効牌は、四七筒・二四五索・西の6種22牌である。
(2)六筒切り
一向聴になる有効牌は、五筒・二四五索・西の5種16牌である。
(3)四索切り
一向聴になる有効牌は、四五六七筒・西の5種16牌である。
従って、五筒切りが牌効率がよい。
暗刻くっつきは、暗刻+単騎、または、雀頭+両搭の両方の側面から捉えることができるので、自由度が高いのである。
・飛び対子の対処。
     
ここから1枚落とさなければならないとしたら、どれを切るか?
(1)二索切り
2を切った場合は、3か4か6(3種8牌)を引いた時に1面子1雀頭が完成する。
(2)四索切り
4を切った場合は、2か3か5か6(4種12牌)を引いた時に1面子1雀頭が完成する。
(3)六索切り
6を切った場合は、2を切った場合と同様3種8牌である。
4を切ることは2や6を切るよりも牌数にして1.5倍も効率がよいことになる。四索切りが牌効率がよい。
麻雀格言で、「飛び対子は間を落とせ」と言われる。1つおきの対子が3つある場合、間の対子を1枚落とせということである。224466持ちの場合には4を1枚切れということである。
・2つの二嵌形
             
自摸状態。伏せ牌部分の6枚では、2面子ができているものとする。
あなたならどれを切るか? 三萬・五萬・七萬・二筒・四筒のどれを切っても一向聴になる。六筒を切った場合だけ、二向聴である。
(1)三萬切りの場合 (七萬切りも同様とみなす)
聴牌になる有効牌は、五萬・六萬・三筒・六筒の4種12牌。
(2)五萬切りの場合
聴牌になる有効牌は、四萬・六萬・三筒の3種12牌。
(3)二筒切りの場合
聴牌になる有効牌は、四萬・六萬の2種8牌。
聴牌になる牌の数だけを数えれば、三萬切りでも五萬切りでも同じなのであるが、正解は三萬切りではなく、五萬切りである。なぜかというと、五萬切りの三五七萬の二嵌形から、両側の両搭に進化しうるからである。
・腹ボテ単騎形か嵌張か
             
自摸状態。伏せ牌部分の6枚では、2面子ができているものとする。
一向聴である。萬子は腹ボテ単騎形であるが、辺搭と両搭の複合とも見ることができる。筒子と索子は嵌張形である。
(1)一萬切り
聴牌に必要な牌は、二筒・四索の2種8牌である。
(2)二萬切り
聴牌に必要な牌は、一筒・二筒・三筒・三索・四索・五索の6種20牌である。
(3)一筒切り
聴牌に必要な牌は、二萬・三筒・四索の3種9牌である。
(4)三索切り
聴牌に必要な牌は、二萬・二筒・五索の3種9牌である。
従って、二萬切りが圧倒的に牌効率がよい。
2枚ある二萬を雀頭にしようと考えると、一二三萬の面子を崩してしまうこととなり、損なのである。因みに、2つの嵌搭においては、一三筒の嵌搭よりも、三五索の嵌搭の方が価値が高い。索子は両側に両搭に進化する可能性があるからである。
・腹ボテ単騎形か腹ボテ二嵌形か
             
自摸状態。伏せ牌部分の6枚では、2面子ができているものとする。
一向聴である。萬子は腹ボテ単騎形であるが、辺搭と両搭の複合とも見ることができる。筒子は腹ボテ二嵌形であるが、嵌搭と嵌搭の複合と見ることができる。
(1)一萬切り
聴牌に必要な牌は、二四筒の2種8牌である。
(2)二萬切り
聴牌に必要な牌は、一二三四五六七筒の7種24牌である。
(3)一筒切り
聴牌に必要な牌は、一二三四萬・三四五六七筒の9種29牌である。
(4)三筒切り
聴牌に必要な牌は、二萬・二四筒の3種10牌である。
従って、一筒切りが牌効率がよい。
二嵌形を崩すことを恐れて牌効率を下げてはいけない。この一向聴の牌姿においては、三筒を雀頭と見据える(決定するではない)ことが、最高の牌効率となる。三筒を雀頭と捉えると、五筒が幅広いくっつき聴牌を狙った浮き牌となることが判る。役のことを考えても、萬子で一盃口ができる可能性が高いのは、一筒切りである。
・搭子多々(1)
             
自摸状態。伏せ牌部分の3枚では、面子ができているものとする。搭子多々状態の二向聴。何を切るのが牌効率がよいか?
このテーマは、単独両搭が3つ、対子が1つ、両搭と対子の複合形が1つで、そのどれを落とすか、という論題とする。
よって、単独両搭落としは三萬切り、対子落としは三筒切り、両搭と対子の複合形落としは四索切り、とする。両搭を嫌って対子を残す三索切りは比較対象に加えない。
(1)三萬切りの場合 (単独両搭落とし)
一向聴になる有効牌は、六九萬・三筒・五八筒・二五索・四索の8種28牌。
(2)三筒切りの場合 (対子落とし)
一向聴になる有効牌は、二五萬・六九萬・五八筒の6種24牌。
(3)四索切りの場合 (両搭と対子の複合形落とし)
一向聴になる有効牌は、二五萬・六九萬・五八筒・二五索の8種32牌。
従って、両搭と対子の複合形を両搭にする四索切りが最も牌効率がよい。
山下さんからご指摘頂いて、修正した。
(2)が正解となっていたが、(3)が正解である。
しかし、この論題は奥が深い。つまり、必ずしも当面の向聴数減少だけを考えるのではなく、その次の自摸も見越して、向聴数を減らさない打ち方もあり、その牌効率の比較は、異なる向聴数の比較となるので、計算が非常に面倒なのである。継続検討課題とする。
因みに、私は、三筒を切りますねぇ。
・搭子多々(2)
          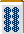   
自摸状態。伏せ牌部分の3枚では、面子ができているものとする。搭子多々状態の二向聴。何を切るのが牌効率がよいか?
このテーマは、単独両搭が4つ、両搭と対子の複合形が1つで、そのどれを落とすか、という論題とする。
よって、単独両搭落としは三萬切り、両搭と対子の複合形落としは両搭を残す四索切り、そして、対子を残す三索切りとする。
(1)三萬切りの場合 (単独両搭落とし)
一向聴になる有効牌は、六九萬・二五筒・六九筒・二五索・四索の9種34牌。
(2)四索切りの場合 (対子落とし)
一向聴になる有効牌は、ない。0種0牌。
(3)三索切りの場合 (対子残し)
一向聴になる有効牌は、二五萬・六九萬・二五筒・六九筒・四索の9種34牌。
従って、四索以外は何を切っても、同じである。
こちらも、「搭子多々(1)」と同様に、牌効率の比較は、異なる向聴数の比較となるので、計算が非常に面倒なのである。継続検討課題とする。
因みに、私は、四索を切りますねぇ。
・延べ単か両面か?
             
自摸状態。伏せ牌部分の6枚では、2面子ができているものとする。三萬・六萬・三筒のどれかを切れば聴牌である。何を切るか?
三萬か六萬切りなら、三六筒の両面待ち、三筒切りなら、三六萬の延べ単(両面単騎)待ちになる。
どれを切っても、両面待ちになり、かつ、待ちは2種6牌である。
では、どれを切っても同じか、というとそうではない。当然、役は考慮しなければならない。残り2面子が暗順ならば平和があるので、三萬か六萬切りとなる。また、三色同順が見込めるならば、それを目指した切り方になるであろう。
ここでは平和も三色同順もないものとする。例えば、中と九索をポンしていて、残る牌がこの8枚というような状況を想定して欲しい。ここで、平和がないのに、延べ単を嫌って、萬子を切る人が多いように感じる。誤っている。
正解は、三筒切りである。三六筒待ちよりも、三六萬待ちの方が出和がりやすいから、である。なぜ、同じ三六の待ちで、2種6牌なのに、三六萬待ちの方が出和がりやすいと言えるのかというと、手残り牌分析の結果による。数牌の3と6では、6の方が7%ほど多く面子構成に寄与する。つまり「使われていて出にくい牌」なのである。萬子の方は三萬3枚と六萬3枚、筒子の方は三筒2枚と六筒4枚であり、同じ6枚でも、3が多い萬子で待つ方が有利なのである。
どれくらい有利かを定量的に示す。単独牌別栄和確率は、
三待ち=0.69%
六待ち=0.60%
である。
(1)三萬切りの三六筒両面待ちの場合
三筒待ち × 2枚 + 六筒待ち × 4枚
=0.69 × 2 + 0.60 × 4 = 3.76%
(2)三筒切りの三六萬延べ単待ちの場合
三萬待ち × 3枚 + 六萬待ち × 3枚
=0.69 × 3 + 0.60 × 3 = 3.86%
従って、(2)の三筒切りの三六萬延べ単待ちの方が出和がりやすい。その比を計算すると2.5%ほど(2)の方が有利である。
このような僅かな差異は、分析と計算を行わなければ算出することはできないし、また体感することもできない。しかし、ほんの僅かな牌効率の違いを知っていれば、対戦数が多ければ多いほど、知っている人と知らない人の差は出てくるものである。
・双ポンか嵌張か?
    
自摸状態。ここに5枚あり、他の9枚で3面子が確定しているものとする。六萬か八萬を切れば聴牌である。何を切るか?
六萬切りなら、八萬と五筒の双ポン待ち、八萬切りなら、七萬の嵌張待ちになる。
一般に、「双ポンより嵌張」と言われる。「これが五筒じゃなくて、もっと端寄りか字牌なら双ポンだけどなあ」と認識している人は多いと思う。
しかし、ここでの例は、五筒である。あなたなら、六萬か八萬か?
正解は、ど真ん中を抱えつつも、双ポン待ちを採る六萬切りなのである。
単独牌別栄和確率は、
五待ち=0.60%
七待ち=0.69%
八待ち=0.95%
である。
(1)六萬切りの八萬と五筒の双ポン待ちの場合
八萬待ち × 2枚 + 五筒待ち × 2枚
=0.95 × 2 + 0.60 × 2 = 3.10%
(2)八萬切りの七萬の嵌張待ちの場合
七萬待ち × 4枚
=0.69 × 4 = 2.76%
従って、(1)の双ポン受けの方がかなり出和がり確率が高いことになる。その比を計算すると、12.3%も双ポン受けの方が有利である。この差はかなり大きい。
「双ポンより嵌張である、その理由は嵌張は両面に変えられるから」と言うことを信じて嵌張待ちにする人は多いようである。事実、この例の場合、六八萬の嵌張受けにしておいて、五萬を引けば四七萬待ちの両面に変わる。しかし、これも認識が誤っている、というか牌効率の悪い打ち方である。
一旦、八萬と五筒の双ポン待ちにしても、その後、四筒か六筒を引けば、両面待ちに変わるのである。四筒か六筒は、2種8枚である。これに対して八萬切りで嵌張受けの場合は五萬、1種4枚を引いた時にしか両面に変わり得ない。つまり、「将来両面に変わる可能性」を考えても、六萬切りで双ポン待ちにしておいた方が有利なのである。
・暗刻か嵌搭か?
    
自摸状態。ここに5枚あり、他の9枚で3面子が確定しているものとする。七萬か五筒(または七筒)を切れば聴牌である。何を切るか?
七萬切りなら六筒の嵌張待ち、五筒切りなら七筒の単騎待ちになる。
「嵌張は4枚あり、単騎は3枚である。従って嵌張の方が有利」と思っている人は多いと思う。
単独牌別栄和確率は、
六待ち=0.60%
七待ち=0.69%
である。
(1)七萬切りの六筒の嵌張待ちの場合
六筒待ち × 4枚
=0.60 × 4 = 2.40%
(2)五筒切りの七筒の単騎待ちの場合
七筒待ち × 3枚
=0.69 × 3 = 2.07%
従って、七萬を切って待ち牌数の多い嵌張待ちにとった方が有利、と計算できる。
しかし、この計算だけで結論を出すのは、浅はかである。もし、この聴牌でどうしても立直をかけなければならない状況であるならば、七萬切りが正解であるが、そうでなければ、よりよい待ちに変化しうるのは、五筒切りの方なのである。これは、「単騎待ちは両面待ちに変わりやすい」と「暗刻持ちの方が多面待ちになりやすい」ということの両方の面から言えることである。
この5枚以外の9枚で3面子が確定している。それが暗順ならば、非常に高い確率で両面または多面待ちに変化しうる。
             
例えば、もしこのような全体牌姿であったならば、五筒を切って七筒単騎待ちを仮聴(かりてん)としておけば、次に、一二四五六八九萬・一二四五六八九索の14種50牌を引けば、2面以上(すべての場合において2種6牌以上)の待ちになる。特に、六萬と八萬と五索を引いた場合には3面待ちとなる。
14種50牌を引けば・・・という確率は、これが平均聴牌巡9巡目だとして、全136牌のうち、自分の持ち牌14牌と自分の捨て牌8牌を除いて104牌を分母として計算すれば、50÷104=48.1%、実に2回に1回は2面以上の待ちに変わることを意味している。
七萬を切って六筒嵌張待ちを仮聴(かりてん)とすることを考えると、四筒か八筒の2種8牌でしか両面待ちに変わり得ない。6.25倍も、五筒切りの方が2面以上の待ちに変わりやすいのである。
五筒を切っても聴牌状態であること、次に高い確率で2面以上の待ちに変わりうること、さらに暗刻持ちは多面待ちに変えやすいことから、五筒切りの方が牌効率がよい、と言える。(注意:厳密には断幺九や平和などの役があるので、和了確率と和了期待点を計算しなければならないが、計算しなくても明らかに五筒切りの方が牌効率がよい)
             
では、こんな全体牌姿だったらどうであろうか。3つ副露をしているので、手の中には自摸状態で5枚しかない。七萬切りと五筒切りで、どちらが牌効率がいいのであろうか。
単独牌別栄和確率は、
五待ち=0.60%
六待ち=0.60%
七待ち=0.69%
八待ち=0.95%
九待ち=1.34%
である。
(1)七萬切りの六筒の嵌張待ちの場合
そのまま六筒で栄和できる確率 2.40%
(a)四筒を引く確率 4÷102=3.92%
三六筒の栄和確率 0.69×4+0.60×4=5.16%
(b)八筒を引く確率 4÷102=3.92%
六九筒の栄和確率 0.60×4+1.34×4=7.76%
2.40+3.92×(5.16+7.76)=2.91%
(2)五筒切りの七筒の単騎待ちの場合
そのまま七筒で栄和できる確率 2.07%
(a)五萬を引く確率 4÷102=3.92%
五六萬の栄和確率 0.60×3+0.60×4=4.20%
(b)六萬を引く確率 4÷102=3.92%
五六八萬の栄和確率 0.60×4+0.60×3+0.95×4=8.00%
(c)八萬を引く確率 4÷102=3.92%
六八九萬の栄和確率 0.60×4+0.95×3+1.34×4=10.61%
(d)九萬を引く確率 4÷102=3.92%
八九萬の栄和確率 0.95×4+1.34×3=7.82%
2.07+3.92×(4.20+8.00+10.61+7.82)=3.27%
従って、他に2面待ちに変わりうる可能性がなくとも、暗刻へのくっつきを期待して、五筒切りで単騎待ちにする方が牌効率がよいことになる。
・両面確定か対子残しか
     
自摸状態。この牌姿は、5を中心に見立てると左右対称形になっているため、三筒切りと七筒切り、四筒切りと六筒切りは同じものと考える。よって低い方、三筒と四筒のどちらを切るべきか、について論じることとする。
「そんなの簡単さあ、四筒より絶対三筒だよ」という声が聞こえてきそうである。事実、この牌姿から三筒を切る人が圧倒的に多い。
三筒切りの場合、面子構成に必要な牌は、二五七八筒の4種14牌である。
四筒切りの場合、面子構成に必要な牌は、三五七八筒の4種12牌である。
よって、三筒切りが正解・・・・・・とは、ならないのである。
平和好きだと言う人の多くは牌効率が悪い。平和好きだと言わない人でも、この場合に無条件で三筒を切る人が多く、それが牌効率がいいと信じてしまっている。
麻雀の牌効率は、和了に向けての最大限有効な捨て牌選択によって決まる。和了には、面子の他に雀頭が必要である。ここに6枚あるということは、残りの牌は8枚である。8枚を2面子+1搭子(または1対子)で考える。
             
伏せ牌部分の6枚では、2面子ができているものとする。この状態で聴牌に向けての有効牌数を考えてみる。
三筒切りの場合、聴牌に必要な牌は、一四萬・二五筒の4種16牌である。
四筒切りの場合、聴牌に必要な牌は、一四萬・三五七八筒の6種20牌である。
よって、四筒切りが有効である。
             
では、2面子+1対子の場合ではどうかを検証する。
三筒切りの場合、聴牌に必要な牌は、二萬・二五七八筒の5種16牌である。
四筒切りの場合、聴牌に必要な牌は、二萬・三五七八筒の5種14牌である。
よって、三筒切りが有効である。
「2面子+1搭子」という場合と、「2面子+1対子」という場合では、それまでの手作りから前者になっているケースが多い。
     
従って、一般論で言えば、この牌姿から、四筒切りが正解なのである。
「両面を多く持っている方が有利」「対子が2つあるのは不利」というのは、総論として正しいが、各論で牌姿によっては必ずしも成り立たないということをしっかりと認識すべきである。「2面子+1搭子」の場合に、三筒を切ってしまうと、六筒が聴牌に寄与しない無駄な牌になってしまうのである。無駄な牌とは、完全孤立牌を無駄自摸することによってのみ生まれるのではない。誤った打ち方をしてしまうことにより、無駄な牌を手牌の中に生み出してしまうのである。そうならないような打ち方がうまい打ち方
、牌効率のいい打ち方である。
・どの対子を落とすか?
             
自摸状態。伏せ牌部分の6枚では、2面子ができているものとする。
三四筒の両搭は落とさないであろう。どの対子を落とすか、である。三萬と四萬は、両搭の複合、つまり、三四萬と三四萬、と見ることができる。その上で三三萬と四四萬という2つの対子にも見ることができる。
このような牌姿から、八索に手がかかる人を見るが、明らかなる誤打なのである。
三萬切りの場合、聴牌に必要な牌は、二四五萬・二五筒・八索の6種20牌である。
八索切りの場合、聴牌に必要な牌は、三四萬・二五筒の4種12牌である。
従って、圧倒的に、三萬切りの方が八索切りよりも牌効率がよい。
・どの対子を落とすか2?
             
自摸状態。伏せ牌部分の6枚では、2面子ができているものとする。
今度は、三萬と五萬の1軒空いている対子の場合である。
五萬切りの場合、聴牌に必要な牌は、三四萬・二五筒・八索の5種16牌である。
八索切りの場合、聴牌に必要な牌は、三五萬・二五筒の4種12牌である。
従って、五萬切りの方が八索切りよりも牌効率がよい。
三萬と五萬との比較では、最終的に双ポン待ちになった時に三萬の方が和了しやすいので、三萬切りではなく五萬切りを正解とした。
・かぶり搭子を落とすか、残すか?
              ドラ: ドラ:
自摸状態。伏せ牌部分の6枚では、2面子ができているものとする。一向聴である。
対子持ちの西がドラであるとする。ドラでなくてもいいのだが、前提条件として、対子は切れない状態での搭子選択の問題である。
三四萬の両搭と、六七萬の両搭と、三四筒の両搭の3つのうち、どれを落とすか?
一般に「かぶり搭子は嫌え」という格言がある。この意味は待ちがかぶる(重なる)搭子は嫌え(落とせ)ということである。同じ牌を2度引かなければならないことを憂慮することから来ている。
この例で言えば、三四萬の両搭と、六七萬の両搭は、五萬がかぶることになり、かぶり搭子である。従って、この格言に従えば、三四萬か六七萬のどちらかの両搭を落とすことになる。
それに対してかぶり搭子を残した方がいいという見解もある。もし五萬を引けば、三面待ちになるから、という理由である。どの搭子を落としても、両面待ちは残る。その両面待ちの中で、三面待ちができる可能性を残す方が有利であるという考え方である。
かぶり搭子は、落とすべきか、残すべきか?
かぶり搭子を落とす場合は四萬切り、かぶり搭子を残す場合は四筒切り、の2点に関して計算する。
単独牌別栄和確率は、
二待ち=0.95%
五待ち=0.60%
八待ち=0.95%
(1)四萬切りの場合(かぶり搭子を嫌う場合)
次の有効牌は、五八萬と二五筒になる。
(a)五八萬を引く確率 8÷102=7.84%
二五筒の栄和確率 0.95×4+0.60×4=6.20%
(b)二五筒を引く確率 8÷102=7.84%
五八萬の栄和確率 0.60×4+0.95×4=6.20%
(7.84×6.20)+(7.84×6.20)=0.97%
(2)四筒切りの場合(かぶり搭子を残す場合)
次の有効牌は、二五八萬になる。
(a)二萬を引く確率 4÷102=3.92%
五八萬の栄和確率 0.60×4+0.95×4=6.20%
(b)五萬を引く確率 4÷102=3.92%
二五八萬の栄和確率 0.95×4+0.60×3+0.95×4=9.40%
(c)八萬を引く確率 4÷102=3.92%
二五萬の栄和確率 0.95×4+0.60×4=6.20%
(3.92×6.20)+(3.92×9.40)+(3.92×6.20)=0.85%
四萬切りの場合(かぶり搭子を嫌う場合)は0.97%、四筒切りの場合(かぶり搭子を残す場合)は0.85%、よって正解は四萬切り(かぶり搭子を嫌う場合)である。
聴牌に向けての有効牌数が、四萬切りの場合は4種類なのに対して、四筒切りの場合は3種類になることで違いが出る。もし、五萬が5枚存在する場合には、三面待ちのメリットがある四筒切りの方が有利となる。
・基本3面待ち絡み
             
自摸状態。伏せ牌部分の3枚では、1面子ができているものとする。
一向聴である。
(1)七萬切り
聴牌に必要な牌は、二五八萬・五八索の5種19牌である。
(2)三筒切り
聴牌に必要な牌は、二五七八萬・四筒・五八索の7種23牌である。
(3)四筒切り
聴牌に必要な牌は、二五筒・五八索の4種16牌である。
従って、三筒切りが牌効率がよい。
四筒切りは、萬子の3面待ちの可能性を断つことになり、愚策である。
七萬切りは、三筒を無駄牌として手の中に生んでしまうことになる。
これらに対して、三筒切りは、七萬を無駄牌としない(七萬が暗刻になっても聴牌)ので、すべての牌を生かすことができる打ち方になる。
・四筒切りか三索切りか?
             
自摸状態。一向聴である。このお題は、小僧さんから頂いた。
和了点数は置いておいて、とにかく早く和がりたい。何を切ればよいか?
役牌中を副露するケースのことを考慮すると複雑になるため、副露はしないものとして、牌効率計算を施すこととする。また、向聴数を増やす中切りも考えられるが、ここでは和了期待点を無視して、早く和了できることを考える。
一向聴状態を保つには、四筒か三索(または七索)を切る必要がある。どちらの牌効率がよいか?
単独牌別栄和確率は、
四待ち=0.60%
五待ち=0.60%
六待ち=0.60%
八待ち=0.95%
である。
(1)四筒切りの場合
次の有効牌は、五八萬と四六索になる。
(a)五八萬を引く確率 8÷102=7.84%
四索または六索の栄和確率 0.60×4=2.40%
(b)四六索を引く確率 8÷102=7.84%
五八萬の栄和確率 0.60×4+0.95×4=6.20%
(7.84×2.40)+(7.84×6.20)=0.67%
(2)三索切り(七索も同様)の場合
次の有効牌は、五八萬と六索になる。
(a)五八萬を引く確率 8÷102=7.84%
六索の栄和確率 0.60×4=2.40%
(b)六索を引く確率 4÷102=3.92%
五八萬の栄和確率 0.60×4+0.95×4=6.20%
(7.84×2.40)+(3.92×6.20)=0.43%
四筒切りの場合は0.67%、三索切り(七索も同様)の場合は0.43%、よって、四筒切りが正解となる。
三索を切る場合、四筒が面子構成に寄与しない無駄な牌になってしまう。四筒を切れば、三五七索の二嵌形が面子構成に寄与する3枚持ち2種待ちとなり、その分、牌効率がよい。三索を切って、無駄な牌、四筒を手牌に生むことのデメリットが計算によって明らかになっている。
・四嵌か三嵌か二嵌か?
        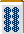      ドラ: ドラ:
自摸状態。3向聴である。俗に言う嵌張地獄である。
このお題はデルガドさんとのディスカッションから生まれた。
萬子は四嵌、筒子は三嵌、索子は二嵌という形になっている。
一般に通常の嵌搭(2枚持ち)と二嵌(3枚持ち)を比較した場合、嵌搭を嫌う方が牌効率がよい。その理由は、二嵌は3枚持ちで2面待ちになっているからである。また、独立した嵌搭2つと二嵌を比較した場合、独立した嵌搭のうち1つを嫌う方が牌効率がよい。独立した嵌搭2つは4枚持ちで2面の待ちなのに対して、二嵌は3枚持ちで2面待ちになっているからである。
同じ4枚持ちで考える。独立した嵌搭2つと三嵌は、どちらも4枚持ちである。そして、独立した嵌搭2つは2面待ちなのに対して、三嵌は3面待ちなので、三嵌の方が有効である。
同様の理由で、二嵌(3枚持ち)と三嵌(4枚持ち)とでは、二嵌を嫌う方が牌効率がよい。その理由は、二嵌が3枚持ち2面待ちなのに対して、三嵌は4枚持ち3面待ちになっているから、である。
| 形 | 持ち牌数 | 待ち数 | 待ち牌/持ち牌 |
| 嵌搭1つ | 2枚持ち | 1面待ち | 50.00% |
| 嵌搭2つ | 4枚持ち | 2面待ち | 50.00% |
| 二嵌 | 3枚持ち | 2面待ち | 66.67% |
| 三嵌 | 4枚持ち | 3面待ち | 75.00% |
| 四嵌 | 5枚持ち | 4面待ち | 80.00% |
しかし、この比較には、他の側面からの検証が必要である。二嵌の場合には3枚持ちで1面子を想定するが、三嵌の場合にそこから1面子を想定する場合と2面子を想定する場合とでは牌効率が大きく異なるからである。上記例の三嵌、二四六八筒において、三筒か七筒を引けば1面子が確定し、2面子めの確定性が高まるが、五筒を引いた場合に、左右対称形となり、2面子めを作るのにあと2牌引かなければならないという事態に陥ってしまう。
よって局所的な例では解明しきれず、全体牌姿からのアプローチを採ることとする。
上記例の3向聴の牌姿から、四嵌を崩すか三嵌を崩すか二嵌を崩すか、どれを崩すのが最も牌効率がよいか、という命題になる訳である。
この牌効率計算の難しいところは、どこで面子ができるかの確定性が保証されないところにある。萬子で2面子・筒子で1面子・索子で1面子が妥当な線であろうと思うが、もし二嵌を崩すことを想定すると絶一門(1色を使わずに他の2色で面子を構成する打ち方)になる可能性が高まる。そうなると、萬子で2面子・筒子で2面子、か、萬子で3面子・筒子で1面子、ということになるのである。
この計算は、両面への手変わりなども考慮しなければならず、非常に複雑であり、手計算では無理である。この問題解析のための専用のプログラムを作らなければ解明できない。今後の課題とする。
 和了期待点 和了期待点
期待値という言葉がある。数学用語である。統計用語とも言える。
『コインを投げて表が出れば80円もらえる。裏が出れば50円もらえる。期待値はいくらか?』という問題に対して、80円×1/2 + 50円×1/2 = 65円 と期待値を計算できるのである。
個別の事象によって期待される値(この場合は円)と、その個別の事象が起こり得る確率をかけたものを、すべての事象において加算すると、期待値が求められる。
世にギャンブル好き、と言われる人たちは、高い手を狙って一か八かの勝負に出る傾向がある。これをギャンブル麻雀と言う。
一般に「高い手は和がる確率は低く、安い手は和がる確率が高い」と言うことができるが、高い手を目指せばよい、安い手を目指せばよい、という単純なことではなく、「ここで高い手に向かった時の和了点と和了確率はいくつで、ここで安い手で行った時の和了点と和了確率はいくつで、従って和了期待点は何点である」という正しい計算ができて、初めて比較ができて、正しい判断が可能になるのである。
手持ち牌として13牌と自摸牌が表示されていて、「さて、何を切りますか?」という問題はよくあるが、これの解答として、有効牌や和了牌の自摸確率、和了牌の栄和確率、和了期待点が示されているものは皆無に近い。
Aを切るのかBを切るのかCを切るのか、どれを切るのが最も得なのか、は、和了期待点を計算することによって、一意な解答を得ることができるのである。
低い可能性でも高い和了点、高い可能性でも低い和了点、どちらを採るのかは、打ち手の性格次第、などという曖昧なものではなく、和了確率と和了期待点によって、明確かつ正確に、「どちらの捨て牌選択の方がどれだけ和了期待点が高い」と定量的かつ客観的に計算できるのである。
麻雀プロや麻雀上級者の言うことが正しいとは限らない。
和了期待点の計算をして判断している人と、そうでなく感覚的かつ曖昧な判断をしている人には、雀力に相当な開きが出る。
和了期待点とは、聴牌時においては簡単に計算できるし、5向聴の配牌時においても(複雑ではあるが)計算できるものである。
「この手牌のうち、何を切るか」という論題において、和了期待点という概念は極めて重要である。非常に簡単に計算できる和了期待点から、例をあげて説明する。
まずは簡単に計算可能な聴牌時の和了期待点を考える。
和了期待点を計算する上において、和了牌別に、そして、栄和/自摸和別に、和了点と、和了確率を出す。
jun巡目、とする。
| 和了牌 | 和了形態 | 和了点 | 残り枚数 | 牌別栄和確率 | 牌別自摸和確率 | 牌別・和了形態別和了期待点 | 牌別和了期待点 | 和了期待点 |
| 和了牌(1) | 栄和 | tensuu[1,1] | maisuu[1] | ronprp[1] | | HOU[1,1]=ronprp[1]×maisuu[1]÷4×(17.5-jun)×tensuu[1,1] | HOU[1]=(HOU[1,1]+HOU[1,2])÷2 | HOU[1]+HOU[2] |
| 自摸和 | tensuu[1,2] | maisuu[1] | | tumprp[1] | HOU[1,2]=tumprp[1]×maisuu[1]÷4×(17.5-jun)×tensuu[1,2] |
| 和了牌(2) | 栄和 | tensuu[2,1] | maisuu[2] | ronprp[2] | | HOU[2,1]=ronprp[2]×maisuu[2]÷4×(17.5-jun)×tensuu[2,1] | HOU[2]=(HOU[2,1]+HOU[2,2])÷2 |
| 自摸和 | tensuu[2,2] | maisuu[2] | | tumprp[2] | HOU[2,2]=tumprp[2]×maisuu[2]÷4×(17.5-jun)×tensuu[2,2] |
栄和か自摸和かによる和了の違いを、和了形態と呼ぶ。
栄和か自摸和かは、和了点数が異なるし、和了確率も異なるので、個別事象として、点数を計算し、和了確率を出す必要があるからである。
牌別栄和確率と、牌別自摸和確率について、詳説する。
牌別自摸和確率については、「次に和了牌(1)を自摸る確率」ということなので、1÷34=2.94%と計算することができる。これは、和了牌が1枚も見えていない場合に次に自摸る確率なのであり、もし河に出ていたり、自分が使っている、また、ドラ表示牌になっているなど、見えている牌、の場合には、残り枚数が減ることとなる。その場合は、枚数を考慮し、牌別自摸和確率を4で割って残り枚数を乗じることによって、自摸和確率を計算する。
牌別栄和確率については、牌別自摸和確率よりもかなり複雑である。端寄りの牌の方が中寄りの牌より捨てられやすいという実戦上の事実を織り込まなければならない。単独牌別の河に捨てられる確率を計算し、さらに、バイロンの法則(栄和は自摸和の2倍であるという法則)補正を計算した上で、
ある巡における他家3人の誰かからの牌別栄和確率を計算した。
| 数牌一 | 数牌二 | 数牌三 | 数牌四 | 数牌五 | 数牌六 | 数牌七 | 数牌八 | 数牌九 | 東 | 南 | 西 | 北 | 白 | 發 | 中 |
| 7.82% | 5.53% | 4.03% | 3.48% | 3.52% | 3.48% | 4.03% | 5.53% | 7.82% | 8.75% | 9.57% | 9.77% | 9.75% | 8.80% | 8.83% | 8.80% |
数牌は、萬子・筒子・索子の色に無関係に上表のようになる。また、数牌の一と九、二と八、三と七、四と六はそれぞれ五を中心に、左右対称となる。
この表の数牌を色の分3倍し、字牌を足すと、200%になる。これは自摸和確率の合計100%に対して、バイロンの法則補正を行った結果である。
つまり、「次に和了牌(1)を自摸る確率」2.94%は普遍的な数値であり、これを基準に、牌別栄和確率を補正計算した結果である。
巡目について。
和了確率は和了できる可能性を表すので、同じ聴牌形でも、巡目が早い方が和了確率は高く、巡目が遅い方が和了確率は低い。初巡に聴牌した場合と、最後の自摸牌で聴牌した場合では、和了確率は全く異なるのである。
牌別栄和確率も牌別自摸和確率も、巡目を基準に計算値を出した。聴牌していて、1巡に和がれる確率というのは、例えば一萬であれば、牌の種類別(牌の枚数別ではなくと言うこと)に、栄和7.82%であり、自摸和2.94%である。
平均の巡数は、17.5巡(東家と南家が18巡、西家と北家が17巡)である。
残り巡が多ければ多いほど比例して和了確率が高まることから、牌別和了確率に、17.5−junを乗じることによって、和了期待点を求める。
和了確率、和了点、巡目によって、牌別・和了形態別和了期待点を計算できる。そして、牌別・和了形態別和了期待点の栄和と自摸和の平均値が、牌別和了期待点
となる。そして、複数の和了牌の牌別和了期待点を合計したものが、和了期待点となる。
             ドラ: ドラ:
この平和聴牌形において、9巡目の和了期待点を計算してみる。
| 和了牌 | 和了形態 | 和了点 | 残り枚数 | 牌別栄和確率 | 牌別自摸和確率 | 牌別・和了形態別和了期待点 | 牌別和了期待点 | 和了期待点 |
 | 栄和 |
立直+平和=2000点 | 4枚 | 3.48% | | 29.58%
591.60点 | 668.97点 | 1384.69点 |
| 自摸和 | 立直+平和+自摸=2700点 | 4枚 | | 2.94% |
27.64%
746.34点 |
 | 栄和 |
立直+平和=2000点 | 4枚 | 4.03% | | 34.26%
685.10点 | 715.72点 |
| 自摸和 | 立直+平和+自摸=2700点 | 4枚 | | 2.94% |
27.64%
746.34点 |
和了期待点は、1384.69点である。これは9巡目における和了期待点であり、同じ牌姿でも、巡目ごとに以下の表のように、和了期待点は変化する。
| 序盤 |
1巡目 | 2巡目 | 3巡目 | 4巡目 |
5巡目 | 6巡目 |
| 2687.93点 | 2525.03点 | 2362.13点 |
2199.21点 | 2036.31点 | 1873.41点 |
| 中盤 | 7巡目 | 8巡目 |
9巡目 | 10巡目 | 11巡目 | 12巡目 |
| 1710.51点 | 1547.59点 | 1384.69点 |
1221.79点 | 1058.89点 | 895.97点 |
| 終盤 | 13巡目 | 14巡目 |
15巡目 | 16巡目 |
17巡目 |
|
| 733.07点 | 570.17点 | 407.27点 |
244.35点 |
81.45点 |
|
もし、上記の平和形が初巡に聴牌したものならば、2687.93点という高い和了期待点になるのであるが、17巡目に聴牌したとすると、たったの81.45点と言う低い和了期待点になる。聴牌が早くても和了できずに巡が進行すれば、それだけ和了期待点は線形に(残り巡数に比例して)下がっていくことになる。
以下に示す和了期待点計算の前提となる条件を列記する。
●聴牌巡目は、最も多い9巡めとする。
●門前時は聴牌即立直するものとする。
●自分にとっての有効牌(和了牌を含む)は場に1枚も出ていないものとする。
●栄和する確率は、自摸和する確率の2倍とする。(バイロンの法則による)
→栄和確率が2÷3、自摸和確率が1÷3、となる。
●流局・他家和了確率を考慮に入れる。
・平和か一盃口か?
              ドラ: ドラ:
9巡目、自摸状態。
聴牌である。二筒を切って三六筒待ちの両面待ち平和に受けるか、五筒を切って嵌三筒待ちの一盃口に受けるか、である。
(1)二筒切りの場合
待ちは三六筒両面待ちの平和となる。
| 和了牌 | 和了形態 | 和了点 | 残り枚数 | 牌別栄和確率 | 牌別自摸和確率 | 牌別・和了形態別和了期待点 | 牌別和了期待点 | 和了期待点 |
 | 栄和 |
立直+平和=2000点 | 3枚 | 4.03% | | 25.69%
513.83点 | 536.79点 | 1205.76点 |
| 自摸和 | 立直+平和+自摸=2700点 | 3枚 | | 2.94% |
20.73%
559.76点 |
 | 栄和 |
立直+平和=2000点 | 4枚 | 3.48% | | 29.58%
591.60点 | 668.97点 |
| 自摸和 | 立直+平和+自摸=2700点 | 4枚 | | 2.94% |
27.64%
746.34点 |
(2)五筒切りの場合
待ちは嵌三筒待ちの一盃口となる。
| 和了牌 | 和了形態 | 和了点 | 残り枚数 | 牌別栄和確率 | 牌別自摸和確率 | 牌別・和了形態別和了期待点 | 牌別和了期待点 | 和了期待点 |
 | 栄和 |
立直+一盃口=2600点 | 3枚 | 4.03% | | 25.69%
667.97点 | 748.62点 | 748.62点 |
| 自摸和 | 立直+一盃口+自摸=4000点 | 3枚 | | 2.94% |
20.73%
829.27点 |
よって、二筒を切って両面に受けた方が和了期待点は1.61倍高い。
平和と一盃口、同じ1飜ならば、符数に差があっても、待ちが広い方を採る方が和了期待点が高く、牌効率がいいことになる。
・一気通貫か平和か?
              ドラ: ドラ:
9巡目、自摸状態。
聴牌である。七萬を切って嵌張五萬待ちという愚形なれど一気通貫を確定させるか、それとも一萬か四萬を切って五八萬待ちの両面待ちの平和とするか?
(1)七萬切りの場合
七萬を切ると、嵌五萬待ちの一気通貫となる。立直+一気通貫である。
| 和了牌 | 和了形態 | 和了点 | 残り枚数 | 牌別栄和確率 | 牌別自摸和確率 | 牌別・和了形態別和了期待点 | 牌別和了期待点 | 和了期待点 |
 | 栄和 |
立直+一気通貫=5200点 | 4枚 | 3.52% | | 29.92%
1555.84点 | 1869.79点 | 1869.79点 |
| 自摸和 | 立直+一気通貫+自摸=7900点 | 4枚 | | 2.94% |
27.64%
2183.74点 |
(2)一萬または四萬切りの場合
一萬または四萬を切ると、五八萬の両面待ちの平和となる。立直+平和である。
| 和了牌 | 和了形態 | 和了点 | 残り枚数 | 牌別栄和確率 | 牌別自摸和確率 | 牌別・和了形態別和了期待点 | 牌別和了期待点 | 和了期待点 |
 | 栄和 |
立直+平和=2000点 | 4枚 | 3.52% | | 29.92%
598.40点 | 672.37点 | 1304.79点 |
| 自摸和 | 立直+平和+自摸=2700点 | 4枚 | | 2.94% |
27.64%
746.34点 |
 | 栄和 |
立直+平和=2000点 | 3枚 | 5.53% | | 35.25%
705.08点 | 632.42点 |
| 自摸和 | 立直+平和+自摸=2700点 | 3枚 | | 2.94% |
20.73%
559.76点 |
よって、ど真ん中の嵌張待ちであっても、七萬切りして一気通貫を確定させた方が有利である。
・七対子か面子手か?
              ドラ: ドラ:
自摸状態。
一向聴である。このような牌姿になって悩んでいる人は多い。七対子の一向聴であり、かつ、面子手の一向聴でもある。面子手に行った場合には一盃口や平和も見える。
「面子手に行く方が牌効率がいいような気もするけど辺張の三萬がなあ」
「いやあ七対子の方が早いかも」
「七対子と面子手を両天秤に取る、四筒切りが一番いいだろう」
「いえいえ、面子手を確定させる六索切りの方が、両面待ちになりやすくていい」
などと考えていても、計算をしなければ答えは出ない。
何を切るのが最も牌効率がいいのか?
これを9巡目だとして、全136牌のうち、自分の持ち牌14牌と自分の捨て牌8牌を除いて104牌を分母として計算する。
単独牌別栄和確率は、
五待ち=0.60%
六待ち=0.60% (四待ちも同様)
七待ち=0.69% (三待ちも同様)
八待ち=0.95%
九待ち=1.34%
である。
(1)三萬切りの場合
七対子を確定させる打ち方となる。七索や八索を切っても計算方式は同様となる。
一向聴から聴牌への有効牌は、四筒・七索・八索の3種9牌となる。
いずれの場合でも、立直+七対子で、3200点が和了点となる。
(a)四筒を引く確率 3÷102=2.94%
七索を切って八索の栄和確率 0.95×3=2.85%
八索を切って七索の栄和確率 0.69×3=2.07%
和了確率が高い方の八索待ちを採択する。
よって、和了期待点は、3200点×2.94%×2.85%=2.68点 となる。
(b)七索を引く確率 3÷102=2.94%
四筒を切って八索の栄和確率 0.95×3=2.85%
八索を切って四筒の栄和確率 0.60×3=1.80%
和了確率が高い方の八索待ちを採択する。
よって、和了期待点は、3200点×2.94%×2.85%=2.68点 となる。
(c)八索を引く確率 3÷102=2.94%
四筒を切って七索の栄和確率 0.69×3=2.07%
七索を切って四筒の栄和確率 0.60×3=1.80%
和了確率が高い方の七索待ちを採択する。
よって、和了期待点は、3200点×2.94%×2.07%=1.95点 となる。
三萬切りの場合、和了期待点は、2.68+2.68+1.95=7.31点 になる。
(2)四筒切りの場合
七対子も面子手も両方を残す打ち方である。
一向聴から聴牌への有効牌は、三萬・七萬・五筒・七索・八索の5種13牌となる。
(a)三萬を引く確率 3÷102=2.94%
六索を切って七萬と五筒の双ポンの栄和確率 0.69×2+0.60×2=2.58%
七索を切って(七対子)八索単騎待ちの栄和確率 0.95×3=2.85%
和了確率は七索切りの方が高いが、和了期待点を計算する。
六索を切って七萬と五筒の双ポン…立直+一盃口
2600×2.58%=67.08点
七索を切って八索単騎待ち…立直+七対子
3200×2.85%=91.20点
和了期待点の高い七索切り採択する。
よって、和了期待点は、3200点×2.94%×2.85%=2.68点 になる。
(b)七萬を引く確率 2÷102=1.96%
六索を切って辺張三萬待ちの栄和確率 0.69×3=2.07%
和了期待点は、立直+一盃口で、2600点×1.96%×2.07%=1.06点 になる。
(c)五筒を引く確率 2÷102=1.96%
六索を切って辺張三萬待ちの栄和確率 0.69×3=2.07%
和了期待点は、立直+一盃口で、2600点×1.96%×2.07%=1.06点 になる。
(d)七索を引く確率 3÷102=2.94%
三萬を切って七対子の八索単騎待ちの栄和確率 0.95×3=2.85%
和了期待点は、立直+七対子で、3200点×2.94%×2.85%=2.68点 になる。
(e)八索を引く確率 3÷102=2.94%
三萬を切って七対子の七索単騎待ちの栄和確率 0.69×3=2.07%
和了期待点は、立直+七対子で、3200点×2.94%×2.07%=1.95点 になる。
四筒切りの場合、和了期待点の合計は、2.68+1.05+1.05+2.68+1.95=9.42点 になる。
(3)五筒切りの場合
七対子を捨てて、面子手を決め打つ打ち方である。
一向聴から聴牌への有効牌は、三萬・三筒・六筒の3種11牌となる。
(a)三萬を引く確率 3÷102=2.94%
六索を切って三六筒の両面待ちの栄和確率 0.69×4+0.60×4=5.16%
和了期待点は、立直+平和+一盃口で3900点×2.94%×5.16%=5.92点 になる。
(b)三筒または六筒を引く確率 8÷102=7.84%
六索を切って辺張三萬待ちの栄和確率 0.69×3=2.07%
和了期待点は、立直+一盃口で2600点×7.84%×2.07%=4.22点 になる。
五筒切りの場合、和了期待点の合計は、5.92+4.22=10.14点 になる。
(4)六索切りの場合
七対子を捨てて、面子手を決め打つ打ち方である。
一向聴から聴牌への有効牌は、三萬・七萬・三筒・六筒・五筒の4種13牌となる。
(a)三萬を引く確率 3÷102=2.94%
五筒を切って三六筒の両面待ちの栄和確率 0.69×4+0.60×4=5.16%
和了期待点は、立直+平和+一盃口で3900点×2.94%×5.16%=5.92点 になる。
(b)七萬を引く確率 2÷102=1.96%
四筒を切って辺張三萬待ちの栄和確率 0.69×3=2.07%
和了期待点は、立直+一盃口で2600点×1.96%×2.07%=1.06点 になる。
(c)三筒または六筒を引く確率 8÷102=7.84%
五筒を切って辺張三萬待ちの栄和確率 0.69×3=2.07%
和了期待点は、立直+一盃口で2600点×7.84%×2.07%=4.22点 になる。
(d)五筒を引く確率 2÷102=1.96%
四筒を切って辺張三萬待ちの栄和確率 0.69×3=2.07%
和了期待点は、立直+一盃口で2600点×1.96%×2.07%=1.06点 になる。
六索切りの場合、和了期待点の合計は、5.92+1.06+4.22+1.06=12.26点 になる。
(5)七索切りの場合
七対子を決め打つ打ち方である。八索切りでも同様の和了期待点となる。
一向聴から聴牌への有効牌は、三萬・四筒・八索の3種9牌となる。
いずれの場合でも、立直+七対子で、3200点が和了点となる。
(a)三萬を引く確率 3÷102=2.94%
四筒を切って八索の栄和確率 0.95×3=2.85%
よって、和了期待点は、3200点×2.94%×2.85%=2.68点 となる。
(b)四筒を引く確率 3÷102=2.94%
三萬を切って八索の栄和確率 0.95×3=2.85%
よって、和了期待点は、3200点×2.94%×2.85%=2.68点 となる。
(c)八索を引く確率 3÷102=2.94%
四筒を切って三萬の栄和確率 0.69×3=2.07%
よって、和了期待点は、3200点×2.94%×2.07%=1.95点 となる。
三萬切りの場合、和了期待点は、2.68+2.68+1.95=7.31点 になる。
             
さあ、これで結果が出た。結果を以下の表にまとめる。
| # | 捨て牌 | 意味 | 役 | 和了点 | 一向聴への牌数 | 和了期待点 |
| (1) |  切り 切り | 七対子決め打ち | 七対子 | 3200点 | 3種9牌 | 7.31点 |
| (2) |  切り 切り | 七対子と面子手両天秤 | 七対子or
一盃口 | 2600点or
3200点 | 5種13牌 | 9.42点 |
| (3) |  切り 切り | 面子手決め打ち | 一盃口or
平和+一盃口 | 2600点or
3900点 | 3種11牌 | 10.14点 |
| (4) |  切り 切り | 面子手決め打ち | 一盃口or
平和+一盃口 | 2600点or
3900点 | 4種13牌 | 1
2.26点 |
| (5) |  切り 切り | 七対子決め打ち | 七対子 | 3200点 | 3種9牌 | 7.31点 |
七対子と面子手を両天秤にかける四筒切りがいいように見えるかもしれないが、一向聴への牌数が13牌で、六索切りと同じものの、和了期待点では3番目になっている。
五筒切りと六索切りは、七対子を捨てるものであるが、七対子を捨てる分、平和の可能性が高くなる。平和は両面待ちなのでその和了確率が高く、結果において和了期待点を上げることになる。五筒か六索かは、普通に考えても六索切りの方が牌効率がよい。
もっとも起こり得る可能性が高いのは、六索を切る→三筒か六筒を引いて聴牌する→五筒を切る→三萬で和了する、というパターンである。四筒を切ってしまうことは、三六筒の受け入れを断つことになり、このデメリットが大きいのである。
よって、牌効率上の最上手は、(4)の六索切り、である。
これは、考えられうる最高点3900点を包含しており、唯一無二の絶対的な解である。
<まだまだ続く>
| ![]() ひいいの麻雀研究
ひいいの麻雀研究